It is well known that every Gaussian integer
![]() can
be uniquely represented as
can
be uniquely represented as
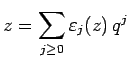 with
with
In particular we prove a central limit theorem for the number of
occurrences ![]() of a given block in the digital expansion of
of a given block in the digital expansion of ![]() (together with asymptotic expansions for the moments and a
local limit theorem) if
(together with asymptotic expansions for the moments and a
local limit theorem) if ![]() and
and
![]() . Further we prove
uniform distribution results in residue classes and modulo 1.
. Further we prove
uniform distribution results in residue classes and modulo 1.
The proofs rely on asymptotic expansion of the generating function
![]() that can be obtained by applying the inverse
Mellin transform on the Dirichlet series
that can be obtained by applying the inverse
Mellin transform on the Dirichlet series
![]() .
.
This work was supported by the Austrian Science Foundation FWF, projects S9604 and S9605.